

One day of the Sudoku puzzles, along with the word search and Scrambled Pun game come from a man named Charles Waterford, a retired school teacher for over 30 years, who creates puzzle books with the help of his grandchildren. With Codewords, numbers are substituted for letters in the crossword grid, and it gives you a few letters to start with. On Saturdays, the crossword puzzle, Str8ts and Sudoku will remain - though the Sudoku games come from new companies - while there will also be a word search and a game called Codewords. Scrambled Puns is similar to the Jumble word game from newspapers of the past. The game provides one letter to give you a start.
#SUDOKU PUZZLES PRINT HOW TO#

Step 1: Start with selecting 15 random locations out of the 81.
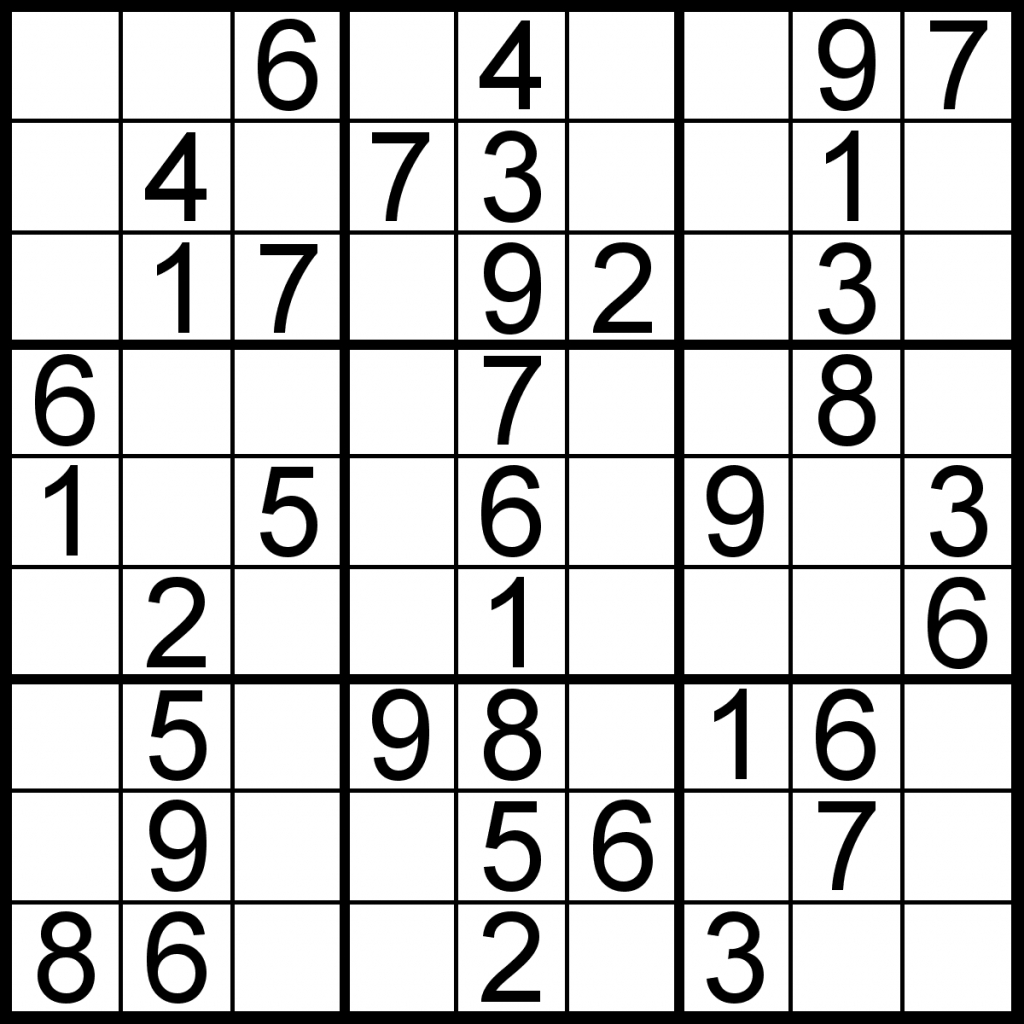
As we already have a quite unique number grid (which is also solved!) this gives us faster performance for using solver Randomly rearrange in 3 row groups of size 3x9ī ) For Masking Pattern we need to have a solver algorithm. Randomly rearrange in 3 column groups of size 9x3 Randomly rearrange rows 7,8 and 9 within themselves Randomly rearrange rows 4,5 and 6 within themselves Randomly rearrange rows 1,2 and 3 within themselves Randomly rearrange columns 7,8 and 9 within themselves Randomly rearrange columns 4,5 and 6 within themselves Randomly rearrange columns 1,2 and 3 within themselves Shuffle the the digits and replace in all other cells Row 7,8,9: Replace the three cell column with the top right column - 3 6 9 and roll within the 3x3 cell for last column Row 4,5,6: Replace the three cell column with the top right column - 2 5 8 and roll within the 3x3 cell for last column Third row is also in ascending order but start from 7 & roll around Second row is also in ascending order but start from 4 & roll around Choose an already exiting matrix, I chose the below one as it can be made easily by human without any help from a computing device or solver: Generating the masking pattern ~ 7e23 combinationsĪ ) For Number pattern the fastest way which can generate unique combinations with NO time spent on backtracing or testing Generating the number pattern 600 billionī. Repeat until the board is completely filled with numbers.Ī.
#SUDOKU PUZZLES PRINT FULL#
Note that this step might produce full valid boards on its own, but those are in no way random. If not, undo step 2 and repeat with another number and cell. Use the backtracking solver to check if the current board has at least one valid solution.
#SUDOKU PUZZLES PRINT FREE#
The first half is to find a complete valid board first (randomly filled!) It works very similar, but "in the other direction":Īdd a random number at one of the free cells (the cell is chosen randomly, and the number is chosen randomly from the list of numbers valid for this cell according to the SuDoKu rules). Of course, this is only the second half of the algorithm. This gives you not only unique boards, but boards where you cannot remove any more numbers without destroying the uniqueness of the solution. Stop when you have tested all 81 positions. If the current board has more than one solution, undo the last removal (step 3), and continue step 3 with the next position from the list If the current board has still just one solution, goto step 3) and repeat. My solver is - in theory - able to count all solutions, but for testing uniqueness, it will stop immediately when it finds more than one solution. Test uniqueness using a fast backtracking solver. Make a list of all 81 cell positions and shuffle it randomly.Īs long as the list is not empty, take the next position from the list and remove the number from the related cell. Start with a complete, valid board (filled with 81 numbers).
Here is the way my own SuDoKu program does it:


 0 kommentar(er)
0 kommentar(er)
